| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 |
- 수학
- 세그먼트 트리
- 브루트포스
- react-three/fiber
- JavaScript
- 티스토리챌린지
- 자료 구조
- 구현
- Next.js
- 시뮬레이션
- three.js
- 코딩일기
- 오블완
- 기본 문법
- State
- 토이 프로젝트
- 엔트리포인트
- 프론트엔드
- js
- 백준
- HTML5
- 자바스크립트
- poiemaweb
- styled-components
- 회고
- 개발 회고
- 자바
- 해시를 사용한 집합과 맵
- 모던 자바스크립트 튜토리얼
- REACT
- Today
- Total
코딩하는 고릴라
[Algorithm] 그래프 표현 - 인접 리스트 구현(JAVA) 본문
그래프 표현 방식 중 하나인 인접 리스트의 구현을 코드를 따라가며 차근차근 이해해보자,,
1. : 가중치가 없는 무향 그래프
1 : 리스트 배열 선언
2 : 리스트 배열 초기화
3 : 연결 정보 저장하기
4 : 요약
2. : 가중치가 있는 그래프의 표현
인접 리스트?
그래프를 다룰 때, 한 정점에서 다른 정점으로의 연결 정보를 리스트 형태로 담아놓은 것이다.
1. 가중치가 없는 무향 그래프의 인접 리스트 표현
먼저, 다음과 같이 4개의 정점(0, 1, 2, 3)이 주어졌으며, 가중치가 없으며 방향성이 없는 무향 그래프를 가정해 보자
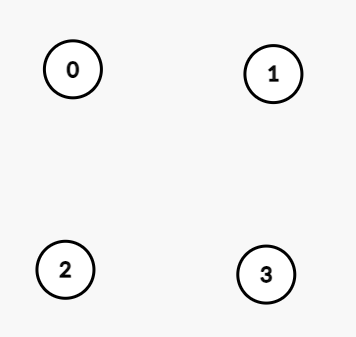
1. 정점의 개수를 입력받고, 이를 길이로 하며 각각의 인덱스에 리스트를 담아 줄 배열을 선언해 준다.
int N = 4; // 정점의 개수로 4가 주어졌다고 가정하자
List<Integer>[] nodes = new ArrayList[N];위 코드에서 처럼 List의 배열을 선언해 줬을 때 nodes 배열의 상태는 아래와 같다.
List의 배열을 선언해 주었으나, 각 인덱스마다 ArrayList를 초기화해주지 않아 기본값인 null이 저장되어 있다.
[단, 정점의 번호가 0번이 아닌 1번부터 시작한다면 배열의 길이를 N+1로 지정해 준다.]

2. 배열의 각 인덱스를 ArrayList로 초기화해 준다.
for (int i = 0; i < nodes.length; i++){
nodes[i] = new ArrayList<>();
}
각 인덱스를 돌며 ArrayList로 초기화해 주면 배열의 각 인덱스에 비어있는 ArrayList들이 저장된다.
이제 문제에서 주어진 입력값을 토대로 연결 정보로 ArrayList들을 채워주기만 하면 된다.
3. 입력받은 연결 정보를 ArrayList에 넣어준다.
문제에서 다음과 같은 입력 정보가 주어졌다고 가정해 보자

첫 줄에 주어진 숫자는 정점과 정점을 연결하는 간선의 숫자(M)가 주어지고,
그 아래줄부터 (시작 정점 - 끝 정점)의 순서로 입력 정보가 주어진다.
첫 줄의 간선 숫자는 일단 무시하고 둘째 줄부터 이어지는 정점과 정점의 연결을 중심으로 살펴보자
(반복문을 이용한 표현을 보고 싶다면, 3-3으로 바로 넘어가자)
3-1. 0번 정점 - 1번 정점 연결
nodes[0].add(1); // 0번 정점에서 1번 정점으로 갈 수 있는 길을 만든다둘째 줄에 주어진 대로, 0번 정점 -> 1번 정점으로의 연결을 지어줬다.
이때 정점 간 연결 상태 및 배열 내 값은 다음과 같다.

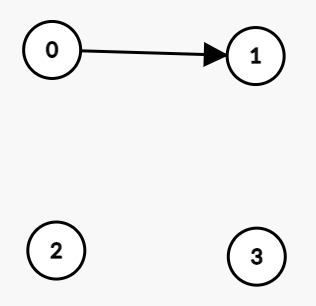
0번 정점에서 1번 정점 방향으로 이어진 것을 알 수 있다.
우리는 방향성이 없는 무향 그래프, 즉 양쪽 정점에서 서로를 오갈 수 있게 표현해야 하니 다음과 같이 코드를 작성해 보자
nodes[0].add(1); // 0번 정점에서 1번 정점으로 갈 수 있는 길을 만든다
nodes[1].add(0); // 반대로, 1번 정점에서 0번 정점으로도 갈 수 있는 길을 만든다
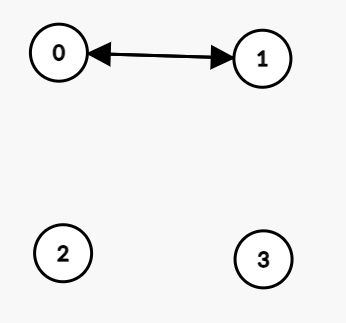
위처럼 코드를 작성하게 되면, 0번과 1번이 서로를 오갈 수 있게 된다.
또한 List 배열에서도 각각 0번 인덱스에 1이, 1번 인덱스에 0이 저장되게 된다.
이는 0번 정점에서 1번 정점으로 갈 수 있고, 1번 정점에서 0번 정점으로 갈 수 있다는 것을 의미한다.
3-2. 남은 정점들도 모두 연결해 보자
// 0번 - 2번 정점의 양방향 연결
nodes[0].add(2);
nodes[2].add(0);
// 1번 - 3번 정점의 양방향 연결
nodes[1].add(3);
nodes[3].add(1);
// 2번 - 3번 정점의 양방향 연결
nodes[2].add(3);
nodes[3].add(2);

위 코드를 통해 연결된 최종적인 그래프의 상태와 List 배열 내 값들이다.
하나하나 연결해 주었던 코드들을 입력이 주어졌을 때 반복문으로 처리하는 코드를 살펴보자
3-3. 반복문을 통한 표현
// 주어진 입력 정보
4
0 1
0 2
1 3
2 3
// M : 한 줄에 주어진 간선의 수를 저장한다.
int M = Integer.parseInt(br.readLine());
// M개의 간선 정보를 저장해야하므로 M번 반복한다.
for (int i = 0; i < M; i++){
// 한 줄 입력 받기
st = new StringTokenizer(br.readLine());
// 입력받은 값에서 앞 정점(시작 정점, start)과 뒤 정점(도착 정점, end)을 각각 변수로 저장한다.
int start = Integer.parseInt(st.nextToken());
int end = Integer.parseInt(st.nextToken());
// start 정점에서 출발해 갈 수 있는 다음 정점 목록(List)에 end를 넣어준다.
nodes[start].add(end);
// 방향이 없는 무향그래프의 경우에는 다음 코드도 작성해 양방향 연결을 만들어준다.
nodes[end].add(start);
}4. 요약
[1단계] : 정점의 개수 입력받기 -> List 배열 선언해 주기
[2단계] : 배열 내 각 인덱스를 ArrayList로 초기화
[3단계] : 각 인덱스 내 배열에 도착 정점 정보 저장
2. 가중치가 있는 그래프
한 정점에서 다른 정점으로 이동할 때의 거리, 비용 등을 계산하는 문제에서는 가중치를 고려해야 한다.
위 과정과 비슷하게 흘러가나 List에 Integer를 저장하지 않고 int[ ] 을 저장하여 풀어나갈 수 있다.
// 입력 정보
4 // 정점의 개수 : 4
// 정점 개수 입력 받기
int N = Integer.parseInt(br.readLine());
// 정점 개수만큼의 크기를 가진 List 배열 선언. 이 때 가중치도 고려해야하므로
// Integer 리스트가 아닌 int[] 리스트를 선언한다.
List<int[]>[] nodes = new ArrayList[N];
// 배열 내 ArrayList 초기화
for (int i = 0; i < nodes.length; i++){
nodes[i] = new ArrayList<>();
}
// 입력 정보
4 // 간선의 개수
0 1 3 // 시작 정점, 도착 정점, 가중치.
0 2 5 // 이번에는 한 쪽 방향으로 이어지는 유향 그래프를 가정해보자
1 3 2
2 3 4
// 간선의 개수 입력받기
int M = Integer.parseInt(br.readLine());
// 간선의 개수만큼 반복
for (int i = 0; i < M; i++){
// 한 줄 입력받기
st = new StringTokenizer(br.readLine());
// 각 정보들을 변수에 저장
int start = Integer.parseInt(st.nextToken());
int end = Integer.parseInt(st.nextToken());
int weight = Integer.parseInt(st.nextToken());
// 시작 정점의 인덱스에 저장된 리스트에 {도착 정점, 가중치} 정보를 int 배열 형태로 저장한다.
nodes[start].add(new int[]{end, weight});
}
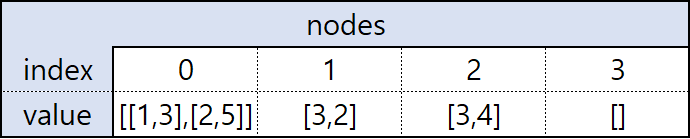
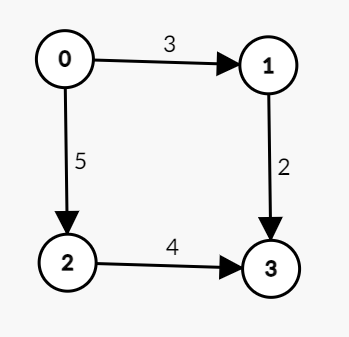
도착 정점과 가중치가 저장된 nodes 배열의 값과 그래프의 상태이다.
nodes[0].get(0)[0] // 1. 도착 정점
nodes[0].get(0)[1] // 3. 1번 정점으로 이동할 때의 가중치위와 같은 방법으로 0번 인덱스에 저장된 도착 정점을, 1번 인덱스에 저장된 가중치를 꺼내어 사용할 수 있다.
🦍
'Algorithm' 카테고리의 다른 글
| [Algorithm] 힙 구현 (Javascript) (0) | 2024.05.24 |
|---|---|
| [Algorithm] 큐 구현(Javascript) (0) | 2023.11.13 |


