| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 |
- HTML5
- 자료 구조
- 엔트리포인트
- 티스토리챌린지
- 해시를 사용한 집합과 맵
- 구현
- styled-components
- js
- 프론트엔드
- 회고
- 세그먼트 트리
- Next.js
- three.js
- 코딩일기
- 브루트포스
- 시뮬레이션
- 모던 자바스크립트 튜토리얼
- REACT
- 개발 회고
- 기본 문법
- poiemaweb
- 수학
- react-three/fiber
- JavaScript
- 자바
- State
- 백준
- 자바스크립트
- 오블완
- 토이 프로젝트
- Today
- Total
코딩하는 고릴라
[Javascript] BOJ_14500. 테트로미노 본문
🦍 문제
14500번: 테트로미노
폴리오미노란 크기가 1×1인 정사각형을 여러 개 이어서 붙인 도형이며, 다음과 같은 조건을 만족해야 한다. 정사각형은 서로 겹치면 안 된다. 도형은 모두 연결되어 있어야 한다. 정사각형의 변
www.acmicpc.net

🐈 문제 풀이
1. 무엇을 구해야 할까?
- 주어진 도형을 회전, 뒤집으면서 도형이 놓인 칸에 쓰여있는 수의 합의 최댓값을 구해야 한다.
2. 어떻게 구해야 할까?
- 배열의 (0, 0) 좌표에서부터 (N, M) 좌표까지 순회하며 각 도형들을 놓고, 회전하고, 뒤집어보며 모든 숫자를 셈한다.
- 각 도형들마다 숫자를 셈하는 함수들을 재귀함수(DFS)로 구현하여 사용했다.
1. 직선 모양
2. Z 모양
3. T 모양
4. L 모양
5. 사각형
2.1. 직선 모양



- 초기 외부에서 함수 호출 시 설정한 방향(_dir)을 유지하며 4칸을 DFS로 탐색
- 4칸 이동 후 (_depth가 3이 됐을 경우), 해당 탐색을 통해 셈한 숫자의 합과 기존에 저장된 숫자를 비교하여 answer 갱신
2.2. Z 모양


- 함수 호출 시 _depth값은 0부터 시작
- Line 20 : 탐색 두번째 칸(_depth === 1) 일 때, 기존 진행방향에서 양쪽으로 90도 꺾어져 탐색
- Line 37 : 탐색 세번째 칸(_depth === 2) 일 때, 초기 진행방향으로 다시 복귀하여 탐색
- Line 13 : 탐색 네번째 칸(_depth === 3) 일 때, 셈한 숫자(_sum)와 answer에 저장된 값을 비교하여 값 갱신
2.3. T 모양

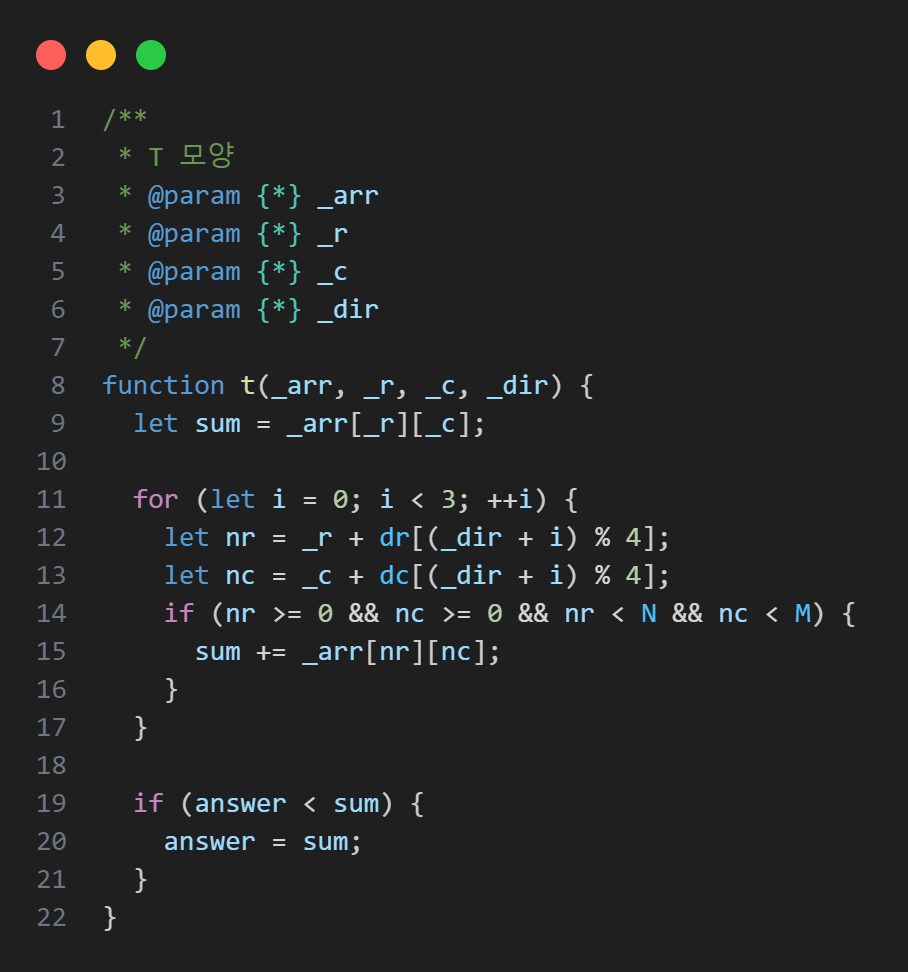
- 탐색은 T자 모양의 중앙에서 시작
- Line 11 : 중앙에서 3방향으로 나뉘어 탐색
2.4. L 모양
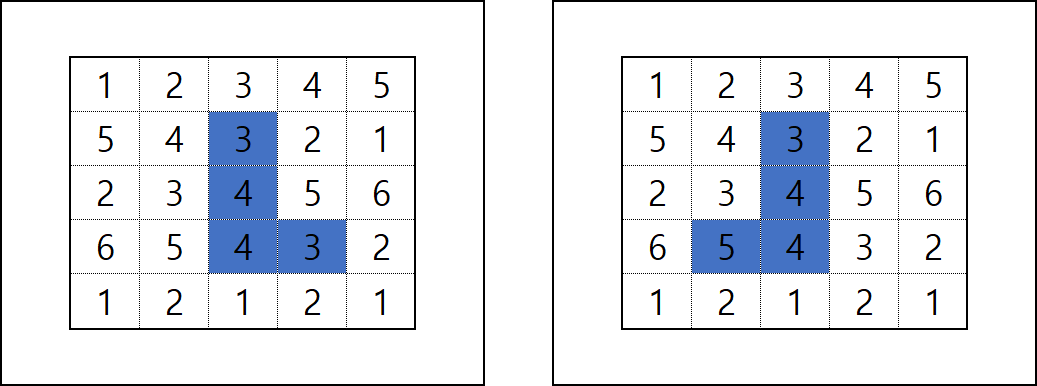

- 초기에는 직선과 같이 첫 진행방향을 유지하며 탐색 진행
- Line 19 : 탐색 세 번째 칸(_depth === 2) 일 때, 진행 방향에서 양쪽으로 90도 꺾어져 탐색
- Line 12 : 탐색 네 번째 칸(_depth === 3) 일 때, _sum과 answer 값을 비교하여 값 갱신
2.5 사각형
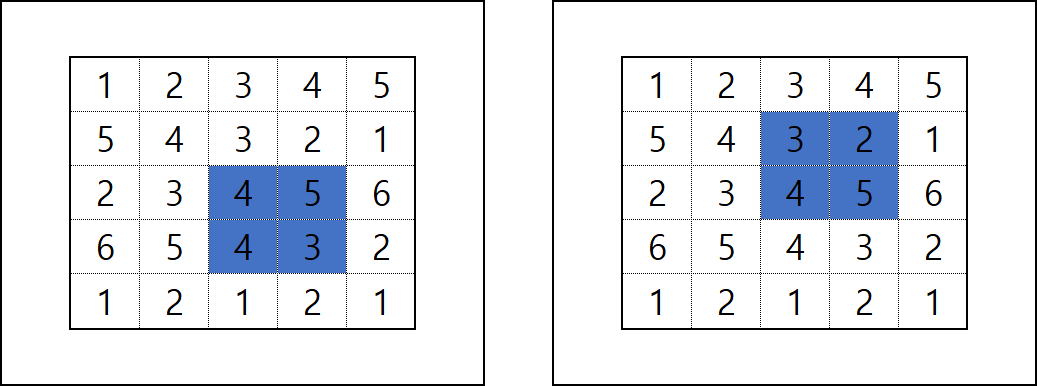

- Line 23 : 매 칸 진행할 때마다 90도씩 진행방향을 꺾어가며 탐색 진행(_depth + 1)
- Line 14 : 탐색 네 번째 칸(_depth === 3) 일 때, _sum과 answer를 비교하여 값 갱신
3. 특별히 고려해야 할 사항은?
- 일일이 매 칸 탐색하는 부분을 구현해줘야 하므로 코드가 상당히 길어질 수 있다,
- 설계한 로직에서 벗어나지 않도록 유의하여 코드를 작성하면 특별히 고려해야 할 부분은 없는 것 같다.
🐕🦺 소스 코드
const input = require("fs").readFileSync("/dev/stdin").toString().split("\n");
const dr = [-1, 0, 1, 0];
const dc = [0, 1, 0, -1];
const [N, M] = input[0].split(" ").map(Number);
let answer = "";
console.log(solution());
function solution() {
const arr = Array(N)
.fill(0)
.map(() => Array(M).fill(0));
for (let i = 1; i <= N; ++i) {
let col = input[i].split(" ").map(Number);
for (let j = 0; j < M; ++j) {
arr[i - 1][j] = col[j];
}
}
for (let i = 0; i < N; ++i) {
for (let j = 0; j < M; ++j) {
// 방향을 지정해 줄 필요가 있는 함수는 방향을 바꿔가며 함수 호출 (linear, Z, T, L)
for (let k = 0; k < 4; ++k) {
linear(arr, i, j, k, 0, arr[i][j]);
z(arr, i, j, k, 0, arr[i][j], k);
t(arr, i, j, k);
L(arr, i, j, k, 0, arr[i][j]);
}
// 방향을 지정해 줄 필요가 없는 사각형 탐색은 매 좌표당 한번만 호출
square(arr, i, j, 0, 0, arr[i][j]);
}
}
return answer;
}
/**
* 직선 모양
* 함수 밖에서 for문을 통해 4방 _dir 지정 필요
* 함수 밖에서 _sum을 arr[r][c]로 지정 필요
* @param {*} _arr
* @param {*} _r
* @param {*} _c
* @param {*} _dir
* @param {*} _depth
* @param {*} _sum
* @returns
*/
function linear(_arr, _r, _c, _dir, _depth, _sum) {
if (_depth === 3) {
if (answer < _sum) {
answer = _sum;
}
return;
}
let nr = _r + dr[_dir];
let nc = _c + dc[_dir];
if (nr >= 0 && nc >= 0 && nr < N && nc < M) {
linear(_arr, nr, nc, _dir, _depth + 1, _sum + _arr[nr][nc]);
}
}
/**
* 사각형
* 함수 밖에서 _dir을 0으로 지정 필요
* 함수 밖에서 _sum을 arr[r][c]로 지정 필요
* @param {*} _arr
* @param {*} _r
* @param {*} _c
* @param {*} _dir
* @param {*} _depth
* @param {*} _sum
* @returns
*/
function square(_arr, _r, _c, _dir, _depth, _sum) {
if (_depth === 3) {
if (answer < _sum) {
answer = _sum;
}
return;
}
let nr = _r + dr[_dir];
let nc = _c + dc[_dir];
if (nr >= 0 && nc >= 0 && nr < N && nc < M) {
square(_arr, nr, nc, _dir + 1, _depth + 1, _sum + _arr[nr][nc]);
}
}
/**
* L 모양
* @param {*} _arr
* @param {*} _r
* @param {*} _c
* @param {*} _dir
* @param {*} _depth
* @param {*} _sum
* @returns
*/
function L(_arr, _r, _c, _dir, _depth, _sum) {
if (_depth === 3) {
if (answer < _sum) {
answer = _sum;
}
return;
}
if (_depth === 2) {
let nDir = (_dir + 1) % 4;
let nr = _r + dr[nDir];
let nc = _c + dc[nDir];
if (nr >= 0 && nc >= 0 && nr < N && nc < M) {
L(_arr, nr, nc, nDir, _depth + 1, _sum + _arr[nr][nc]);
}
nDir = _dir - 1 >= 0 ? _dir - 1 : _dir + 3;
nr = _r + dr[nDir];
nc = _c + dc[nDir];
if (nr >= 0 && nc >= 0 && nr < N && nc < M) {
L(_arr, nr, nc, nDir, _depth + 1, _sum + _arr[nr][nc]);
}
return;
}
let nr = _r + dr[_dir];
let nc = _c + dc[_dir];
if (nr >= 0 && nc >= 0 && nr < N && nc < M) {
L(_arr, nr, nc, _dir, _depth + 1, _sum + _arr[nr][nc]);
}
}
/**
* Z 모양
* @param {*} _arr
* @param {*} _r
* @param {*} _c
* @param {*} _dir
* @param {*} _depth
* @param {*} _sum
* @param {*} _oDir
* @returns
*/
function z(_arr, _r, _c, _dir, _depth, _sum, _oDir) {
if (_depth === 3) {
if (answer < _sum) {
answer = _sum;
}
return;
}
if (_depth === 1) {
let nDir = (_dir + 1) % 4;
let nr = _r + dr[nDir];
let nc = _c + dc[nDir];
if (nr >= 0 && nc >= 0 && nr < N && nc < M) {
z(_arr, nr, nc, nDir, _depth + 1, _sum + _arr[nr][nc], _oDir);
}
nDir = _dir - 1 >= 0 ? _dir - 1 : _dir + 3;
nr = _r + dr[nDir];
nc = _c + dc[nDir];
if (nr >= 0 && nc >= 0 && nr < N && nc < M) {
z(_arr, nr, nc, nDir, _depth + 1, _sum + _arr[nr][nc], _oDir);
}
return;
}
if (_depth === 2) {
let nr = _r + dr[_oDir];
let nc = _c + dc[_oDir];
if (nr >= 0 && nc >= 0 && nr < N && nc < M) {
z(_arr, nr, nc, _dir, _depth + 1, _sum + _arr[nr][nc], _oDir);
}
return;
}
let nr = _r + dr[_dir];
let nc = _c + dc[_dir];
if (nr >= 0 && nc >= 0 && nr < N && nc < M) {
z(_arr, nr, nc, _dir, _depth + 1, _sum + _arr[nr][nc], _oDir);
}
}
/**
* T 모양
* @param {*} _arr
* @param {*} _r
* @param {*} _c
* @param {*} _dir
*/
function t(_arr, _r, _c, _dir) {
let sum = _arr[_r][_c];
for (let i = 0; i < 3; ++i) {
let nr = _r + dr[(_dir + i) % 4];
let nc = _c + dc[(_dir + i) % 4];
if (nr >= 0 && nc >= 0 && nr < N && nc < M) {
sum += _arr[nr][nc];
}
}
if (answer < sum) {
answer = sum;
}
}
🐖 Think
- 코드 길이가 매우 길어서 힘들었는데, 각 기능별 필요한 기능을 미리 설계해 두고 이를 따라가는 식으로 진행하다 보니 문제 풀이에 오점이 발생하지는 않았다.
'APS' 카테고리의 다른 글
| [Java] BOJ_1541. 잃어버린 괄호 (0) | 2024.02.11 |
|---|---|
| [Javascript] BOJ_20055. 컨베이어 벨트 위의 로봇 (1) | 2023.12.30 |
| [Javascript] BOJ_17144. 미세먼지 안녕! (0) | 2023.12.18 |
| [Javascript] BOJ_4673. 셀프 넘버 (2) | 2023.11.25 |
| [JAVA] BOJ_14499. 주사위 굴리기 (0) | 2023.11.04 |




