| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- JavaScript
- 시뮬레이션
- 코딩일기
- 자바스크립트
- State
- 토이 프로젝트
- 세그먼트 트리
- 프론트엔드
- 해시를 사용한 집합과 맵
- 자바
- 백준
- js
- REACT
- 엔트리포인트
- 오블완
- Next.js
- react-three/fiber
- 모던 자바스크립트 튜토리얼
- 수학
- 개발 회고
- 티스토리챌린지
- 자료 구조
- poiemaweb
- 구현
- three.js
- styled-components
- 기본 문법
- HTML5
- 회고
- 브루트포스
- Today
- Total
코딩하는 고릴라
[JAVA] BOJ_7626. 직사각형 본문
🐒 문제
7626번: 직사각형
첫째 줄에 양의 정수 N이 주어진다. (1 ≤ N ≤ 200,000) 다음 N개 줄에는 공백으로 나누어진 네 값 "x1, x2, y1, y2"가 주어진다. 이 값은 직사각형 [x1,x2] × [y1,y2]를 나타낸다. 모든 좌표는 0보다 크거나
www.acmicpc.net
🐈 풀이
1. y좌표 압축
2. x축 정렬 후 x축 방향으로 순차적으로 스위핑
3. 스위핑하며 직사각형의 세로선 활성화 및 비활성화를 통해 좌표상의 직사각형 넓이를 구한다.
1. 주어지는 x, y 좌표의 최대값이 매우 커 이를 바로 활용해 트리를 만들 수 없다. 따라서 좌표 압축을 필요로 한다.
2. 스위핑 기법을 통해 문제풀이를 진행하되, 과연 어떤 값을 어떻게 저장하고 꺼내와야 하는지의 아이디어가 중요했다.
- 잘못된 방법으로 주구장창 붙잡고만 있었다,,
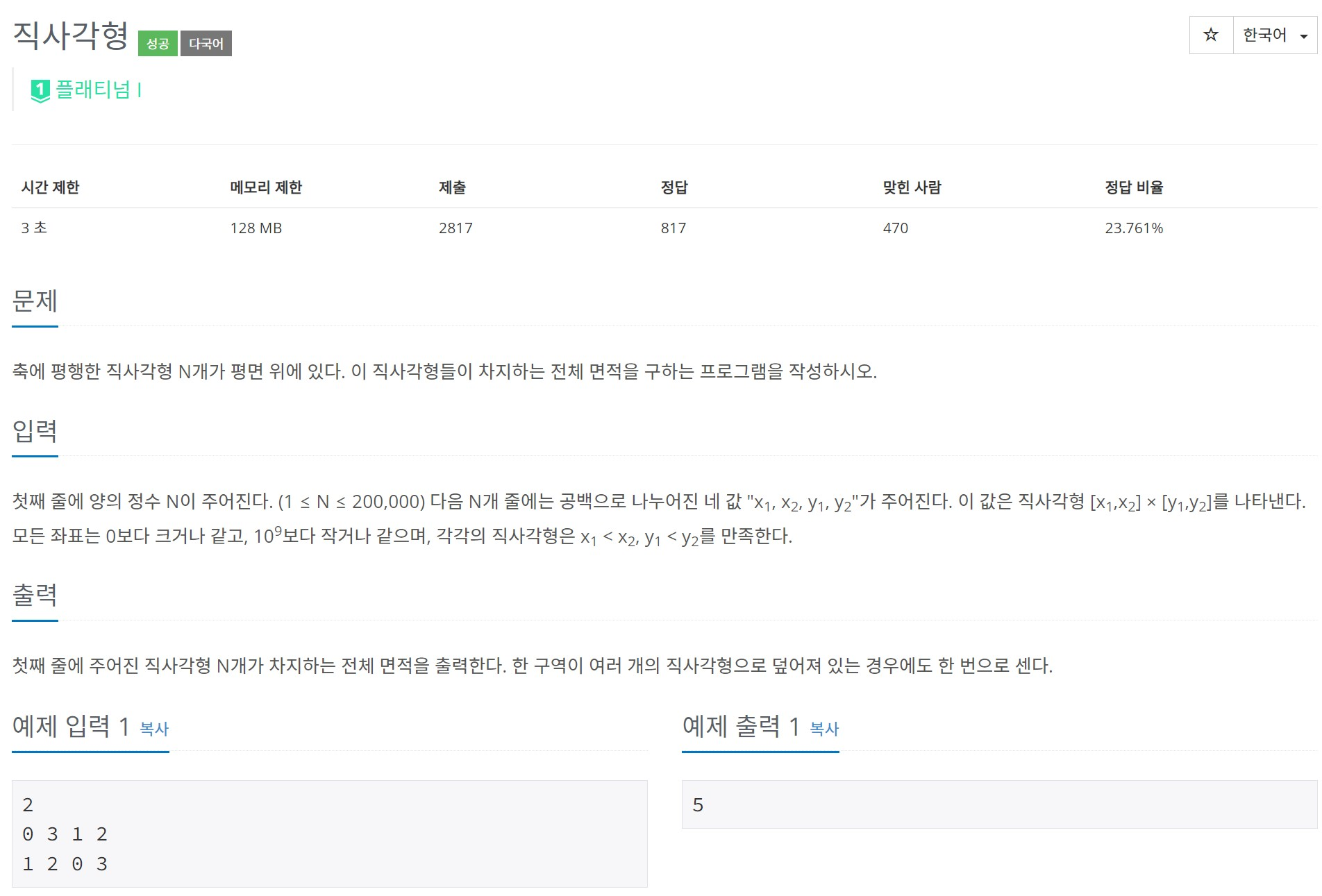
아래는 해당 문제를 어떤 식으로 풀어나가야 할 지에 대해 구체적인 설명은 없는,,, 대략적인 모식도이다.
코드를 보면 머리가 좀 복잡복잡 해지는데 아래 사진들을 보면 시각적으로 이해가 조금은 될 것 같다.
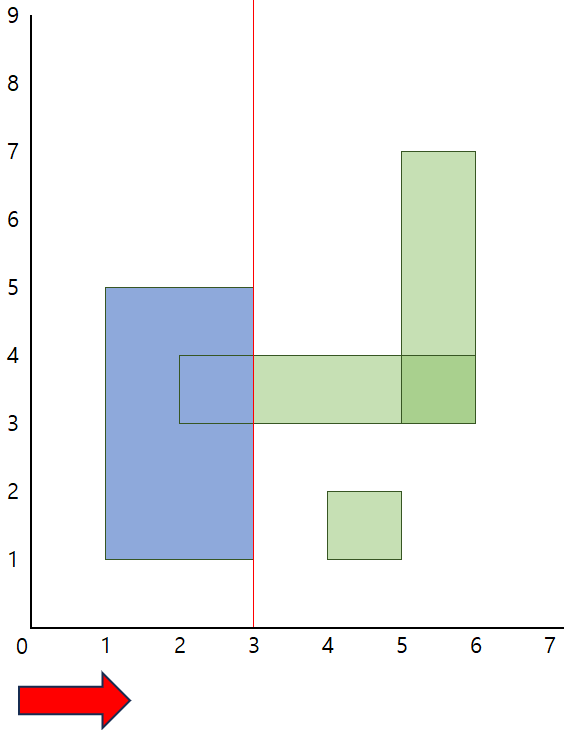
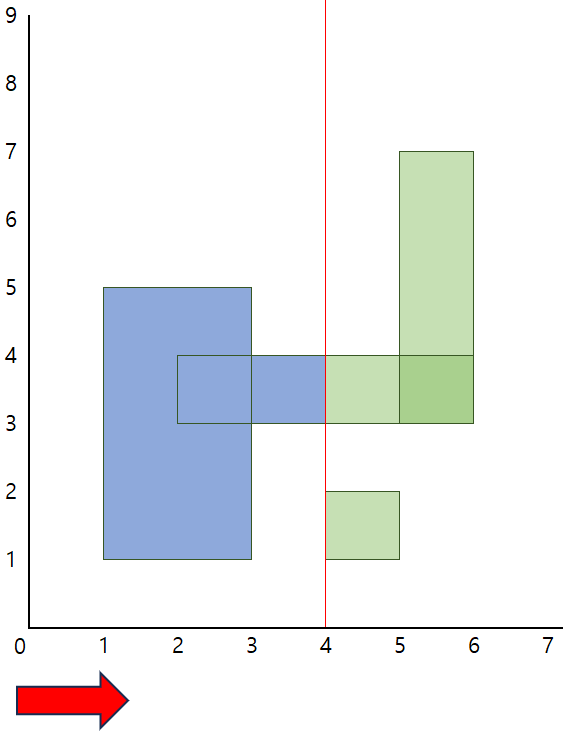
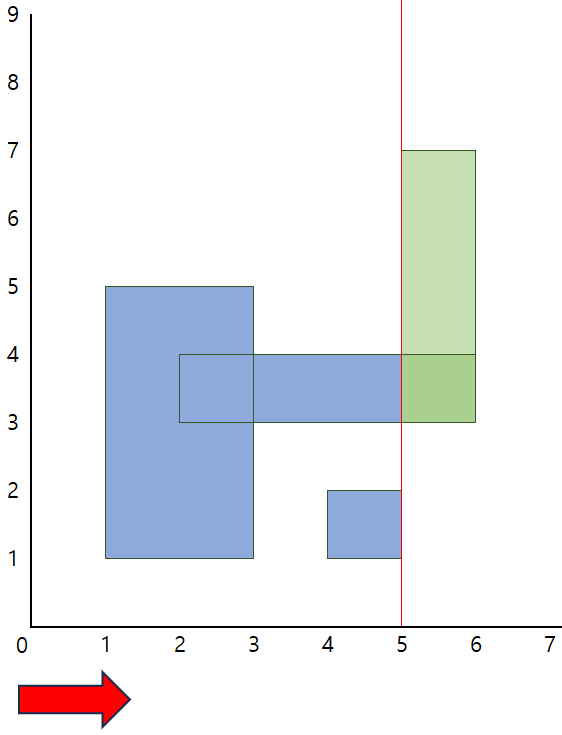
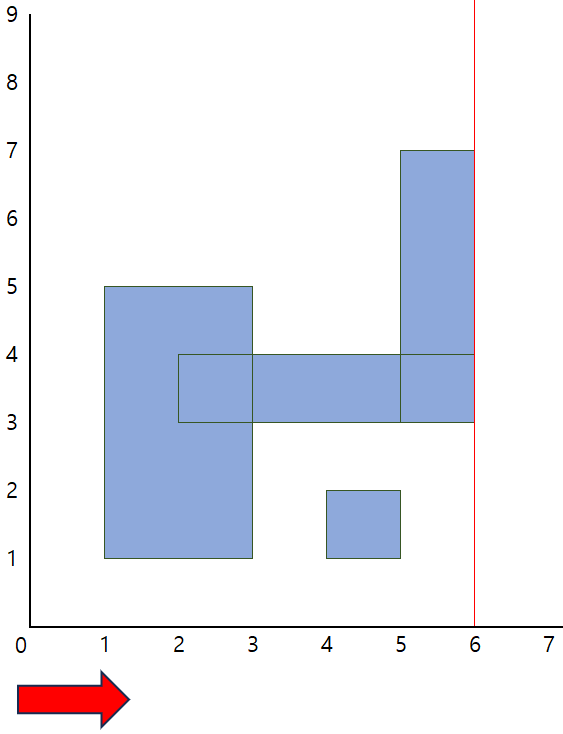
위 슬라이드 쇼 내 사진들은 y축 좌표의 압축은 이루어지지 않은 상태이다.
이 상태에서 각 과정을 설명하자면, 먼저 평면상의 직사각형들을 좌측에서부터 훑어간다.
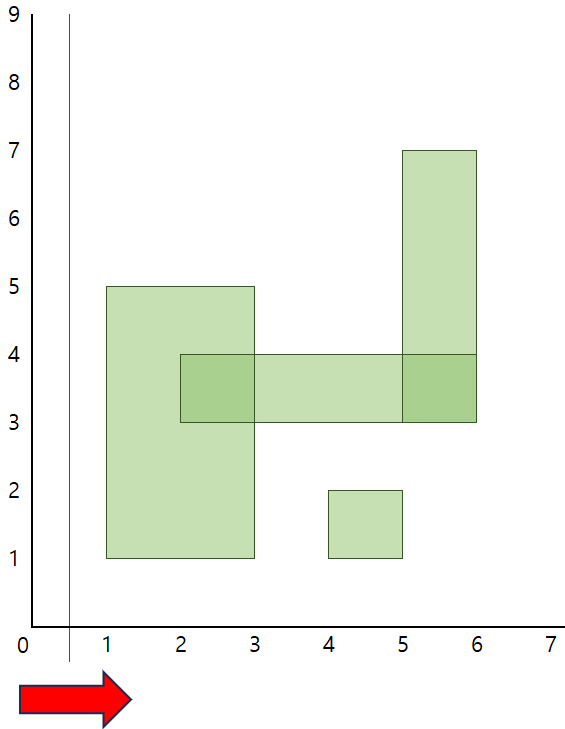
1) x = 1일 때, 직사각형의 시작지점을 만났고 이 때 직사각형 세로선의 길이는 1~5로 4의 길이를 가지고 있다.
해당 상황에서 해당 선을 활성화 상태로 둔다. 활성화 상태로 둔 선은 다음 세로선을 만났을 때 직사각형의 넓이 계산에 사용된다.
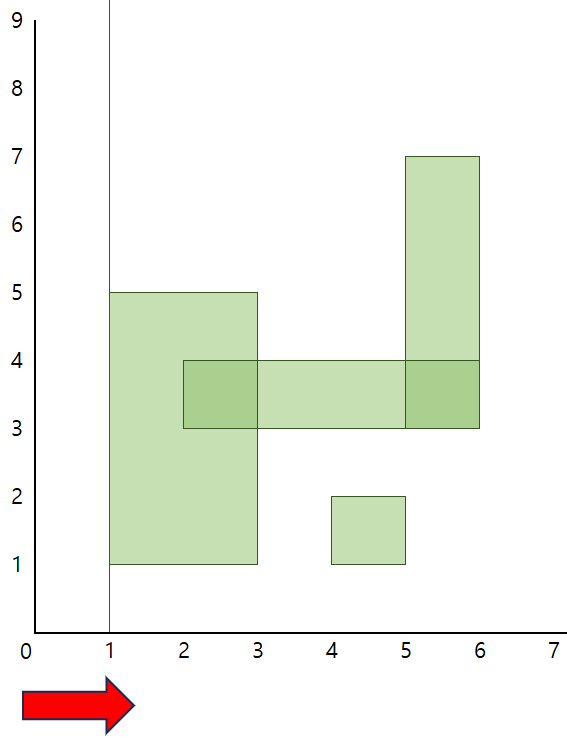
2) x = 2일 때, 빨간 선은 두번째 세로선을 만난다.
이 때, (활성화된 세로선의 길이 * x축으로의 변화량)의 결과값을 result 변수에 더해 저장해준다. 따라서 파란색으로 칠해진 직사각형은 계산된 넓이가 된다.
3) x = 3일 때, 빨간 선은 그 다음 세로선을 만났고, 이는 첫번째 직사각형의 종료 지점이다.
이 때 겹쳐있지 않은 세로선(y값 : 1~3, 4~5)은 비활성화 시켜주고, 겹쳐져 있어 아직 살아있는 세로선(y값 : 3~4)은 활성화 상태로 둔다. 과정 2와 마찬가지로 또 다른 세로선을 만났으므로 활성화된 세로선의 길이와 x축 변화량을 통해 넓이를 계산하여 변수에 더해 저장해둔다.
4...) 위와 같은 과정들을 거쳐 끝까지 훑게되면 직사각형의 넓이를 구할 수 있다.
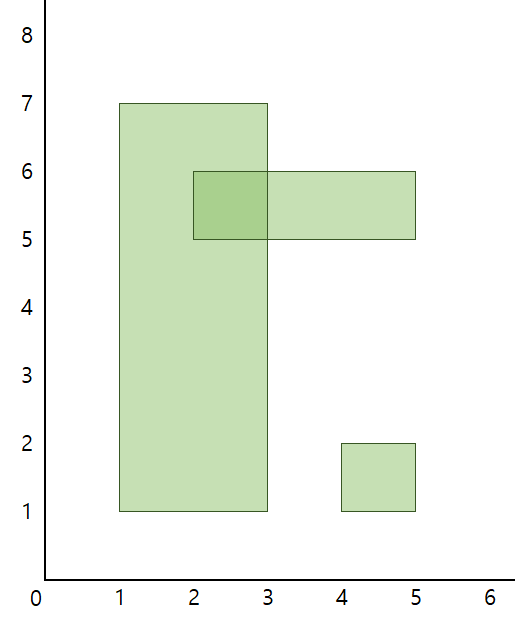
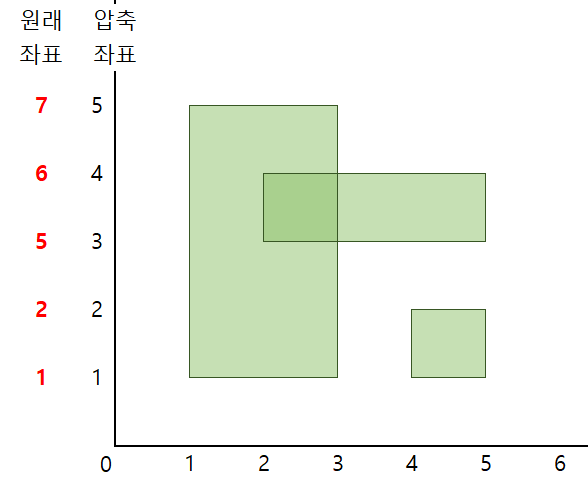
위 사진은 좌표 압축 전/후의 y좌표값 변화이다. 왼쪽의 직사각형을 좌표압축하면 우측과 같이 변하게 되며, 이 때 원래 좌표의 값을 따로 저장해두어, 압축된 좌표를 통해서도 y축 길이를 구할 수 있도록 한다.
- 트리를 이차원 배열로 선언했다.
- 트리의 [0]번 인덱스에는 활성화된 세로선의 압축 전 길이를, [1]번 인덱스에는 활성화된 직사각형의 개수를 저장한다.
- 활성화된 직사각형의 개수가 0개인 구간의 세로선의 길이는 0으로 초기화시킨다.
- 트리에는 y축 값이 들어가는 것이 아니고, y값 사이의 구간별 길이를 담는다.
- 따라서 압축된 y값이 5개 존재한다면, 트리에 저장될 리프노드 값은 4개가 존재한다.
public void update(int node, int start, int end, int left, int right, int val);
update(1, 0, N*2-1, low, high-1, 1);- y축 값의 압축은 0번부터 사용하도록 진행하였고, 따라서 update메서드 내 매개변수값으로는 위 처럼
- node = 1, start = 0, end = N * 2 - 1, left = y1, right = y2 - 1, val = (1 or -1) 이 들어간다.
- val 값은 직사각형의 활성화/비활성화할 때 사용한다. 활성화 할때 1, 비활성화 할때 -1값을 사용한다.
🐕🦺 소스 코드
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.ArrayList;
import java.util.Collections;
import java.util.Comparator;
import java.util.HashMap;
import java.util.List;
import java.util.Map;
import java.util.StringTokenizer;
public class Main {
static int N;
static int[] compOriginArr;
static long[][] tree;
static List<int[]> pos;
static Map<Integer, Integer> comp;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
StringBuilder sb = new StringBuilder();
// N : 직사각형 개수
N = Integer.parseInt(st.nextToken(" "));
// pos : {x좌표, y좌표, 높이} 를 담아주는 List
pos = new ArrayList<>();
// 좌표를 받아 List에 2차원 배열 형태로 저장하기
for (int i = 0; i < N; i++) {
st = new StringTokenizer(br.readLine());
int x1 = Integer.parseInt(st.nextToken(" "));
int x2 = Integer.parseInt(st.nextToken(" "));
int y1 = Integer.parseInt(st.nextToken(" "));
int y2 = Integer.parseInt(st.nextToken(" "));
// y2 - y1 : 해당 x좌표에서 직사각형의 높이
pos.add(new int[] { x1, y1, y2 }); // [1] : y1 / [2] : y2 => 직사각형의 시작지점
pos.add(new int[] { x2, y2, y1 }); // [1] : y2 / [2] : y1 => 직사각형의 종료지점
}
// comp : 좌표 압축을 위한 HashMap
comp = new HashMap<>();
// compOriginArr : 압축 이전의 원래 좌표를 넣을 HashMap
compOriginArr = new int[pos.size()];
// y축 정렬
Collections.sort(pos, new Comparator<int[]>() {
@Override
public int compare(int[] o1, int[] o2) {
return o1[1] - o2[1];
}
});
// y축 압축
int idx = -1;
for (int i = 0; i < pos.size(); i++) {
int[] cur = pos.get(i);
if (!comp.containsKey(cur[1])) {
comp.put(cur[1], ++idx);
}
compOriginArr[idx] = cur[1];
cur[1] = comp.get(cur[1]);
}
// x축 정렬
Collections.sort(pos, new Comparator<int[]>() {
@Override
public int compare(int[] o1, int[] o2) {
return o1[0] - o2[0];
}
});
// N개의 직사각형이 존재할 때, 직사각형의 시작, 종료지점은 N * 2개 존재
int h = (int) Math.ceil(Math.log(N * 2) / Math.log(2));
int size = 1 << h + 1;
tree = new long[size][2];
// res : 결과를 담을 변수
long res = 0;
// x축 방향으로 쭉 훑으면서 진행한다.
// pre : 직전의 좌표를 담을 변수
int[] pre = new int[] { 0, 0, 0 };
for (int i = 0; i < pos.size(); i++) {
// cur : 현재 좌표
int[] cur = pos.get(i);
// cur[1]은 압축하면서 압축된 값으로 저장해둬 바로 가져오면 됨
int low = cur[1];
// cur[2]는 따로 압축된 값으로 저장하지 않아 압축값이 담긴 HashMap에서 값을 가져온다.
int high = comp.get(cur[2]);
// tree[1][0] : 현재 상황에서, 활성화된 세로 선분의 길이
// (cur[0] - pre[0]) : 현재 x좌표 - 직전의 x좌표. 즉 x축 방향으로의 너비.
// res : 높이 * 너비 = 넓이
res += tree[1][0] * (cur[0] - pre[0]);
// ArrayList에 좌표값을 넣어둘 때, 직사각형의 종료지점은 low가 high보다 크게끔 저장을 했다.
// low > high : 직사각형의 종료 지점
if (low > high) {
// 마지막 매개변수에 -1을 담아 활성화된 직사각형 개수를 1 줄임
update(1, 0, N * 2 - 1, high, low - 1, -1);
}
// else : 직사각형의 시작 지점
else {
// 마지막 매개변수에 1을 담아 활성화된 직사각형 개수를 1 늘림
update(1, 0, N * 2 - 1, low, high - 1, 1);
}
// 직전의 좌표를 현재의 좌표로 갱신시킨다.
pre = cur;
}
System.out.println(res);
}
static void update(int node, int start, int end, int left, int right, int val) {
// 찾고자 하는 범위를 벗어났다면 리턴
if (end < left || right < start) {
return;
}
// 중간 점 구하기
int mid = (start + end) / 2;
// 해당 구간 범위에 들어왔다면
if (left <= start && end <= right) {
// 해당 구간의 세로 선을 활성화시킨다.
tree[node][1] += val;
}
// 범위에서 벗어났다면
else {
update(node * 2, start, mid, left, right, val);
update(node * 2 + 1, mid + 1, end, left, right, val);
}
// 해당 구간에 세로 선이 하나 이상 활성화 됐다면
if (tree[node][1] != 0) {
// 해당 구간의 세로 길이를 저장한다.
tree[node][0] = compOriginArr[end + 1] - compOriginArr[start];
}
// 해당 구간에 선이 모두 죽어있다면
else {
// 리프 노드일 때만
if (start == end) {
// 해당 구간의 선을 비활성화 시킨다(값을 초기화시킨다)
tree[node][0] = 0;
} else {
// 리프노드가 아니라면 자손 노드의 값들을 더해준다.
tree[node][0] = tree[node * 2][0] + tree[node * 2 + 1][0];
}
}
}
}
🐖 Think
- 세그먼트 트리의 값을 조작하는 update메서드 내부의 코드를 유동적으로 짜는 것이 어려웠다. 기존에는 항상 쓰던대로 작성했었는데 상황에 맞게 조작할 줄 아는 것이 중요할 것 같다.
- 또한 설명이 되게,,, 많이 어려운 문제인 것 같다. 풀이를 논리정연하게 정리할 수 있는 능력 또한 필요할 것 같다.
'APS' 카테고리의 다른 글
| [JAVA] BOJ_1269. 대칭 차집합 (0) | 2023.10.26 |
|---|---|
| [JAVA] BOJ_19236. 청소년 상어 (1) | 2023.10.19 |
| [JAVA] BOJ_3055. 탈출 (0) | 2023.10.17 |
| [JAVA] BOJ_1654. 랜선 자르기 (1) | 2023.10.10 |
| [JAVA] BOJ_9435. 디지털 비디오 디스크(DVDs) (2) | 2023.10.10 |




